Functional programming II

In this lesson, we’ll continue to practice functional programming in R. To give us something to work on, we’ll code up our own version of a k-means clustering algorithm. R already has a function to do this, appropriately titled kmeans(), but we’ll pretend it doesn’t.

Being able to code up an algorithm based on mathematical notation or pseudocode is a really valuable skill to possess. As algorithms become even moderately complex, however, leaning on quick and dirty spaghetti code to “just get the job done” quickly becomes a mess. When you’ve worked hard to get an algorithm to work, it’s important to work a little harder to write it in a functional way that

Makes it clear what you have done (self-documenting);
Is easily ported to another project.

With these goals in mind, we’ll write our own k-means clustering function. Because this lesson isn’t about learning the ins and outs of machine learning, we won’t dive into the various robustness checks we might otherwise perform were this a real project. That said, we should be able to write a well-performing function.

Load libraries and set paths

## ---------------------------
## libraries
## ---------------------------
library(tidyverse)

## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──

## ✔ ggplot2 3.3.5     ✔ purrr   0.3.4
## ✔ tibble  3.1.6     ✔ dplyr   1.0.8
## ✔ tidyr   1.2.0     ✔ stringr 1.4.0
## ✔ readr   2.1.2     ✔ forcats 0.5.1

## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()

library(plotly)

## 
## Attaching package: 'plotly'

## The following object is masked from 'package:ggplot2':
## 
##     last_plot

## The following object is masked from 'package:stats':
## 
##     filter

## The following object is masked from 'package:graphics':
## 
##     layout

As always, we are working in the ./scripts subdirectory.

## ---------------------------
## directory paths
## ---------------------------

## assume we're running this script from the ./scripts subdirectory
dat_dir <- file.path("..", "data")

Read in and inspect data

## ---------------------------------------------------------
## read in data
## ---------------------------------------------------------

df <- readRDS(file.path(dat_dir, "kmeans.RDS"))

## show
df

## # A tibble: 1,500 × 3
##        x     y     z
##    <dbl> <dbl> <dbl>
##  1 33.1  11.6  -16.0
##  2 -8.55  6.01  11.8
##  3 50.7  56.3   97.8
##  4  2.83 27.5   34.4
##  5 -4.66 20.0   25.1
##  6 -3.04 16.2   22.8
##  7 30.5  12.1  -14.3
##  8  7.08 25.3   25.6
##  9  1.33 20.1   17.6
## 10 -3.11 13.4   11.5
## # … with 1,490 more rows

The data set is an 1,500 by 3 matrix, with three covariates (or features in machine learning parlance), x, y, and z. Since these columns names don’t tell us much, let’s plot the first two features against each other in a scatter plot.

## plot first two dimensions
g <- ggplot(df, mapping = aes(x = x, y = y)) + geom_point()

## show
g

plot of chunk programming_two_data

While there appears to be an overall positive correlation between x and y, the data seem to cluster into three groups. One group (furthest left on the x axis) seems more distinct from the other two, which look to be on the same trend line, but clumped in lower and higher positions.

Our task will be to assign each point to an as yet unspecified group with the goal that each group will be contiguous (e.g., will cluster together).

K-means clustering

Formally, the objective function for a k-means clustering algorithm is as follows (from Wikipedia):

\[ \underset{S}{arg\,min} \sum_{i=1}^k\sum_{x\in S_i} \vert\vert x - \mu_i \vert\vert^2\]

where

\(k\) is the number of clusters
\(S_i\) is one cluster set of points
\(\vert\vert x - \mu_i \vert\vert^2\) is the squared Euclidean distance

In English, the objective is that for a fixed number of clusters, assign each point to a cluster such the variance within each cluster (within-cluster sum of squares or WCSS) is minimized. If you think that this sounds like the objective of ordinary least squares (OLS), you are right. The difference here is that instead of creating a line of best fit (or using parametric assumptions to make inferences), we are simply assigning each point to its “cluster of best fit.”

Algorithm

There are number of algorithms to compute k-means. We’ll use Lloyd’s algorithm, which isn’t the best, but is the simplest and works well enough for our purposes.

Choose number of clusters, \(k\).
Randomly choose \(k\) points from data to serve as initial cluster means.
Repeat following steps until assignments no longer change:
1. Assign each point to the cluster with the closest mean (see Step 3.1, below, for formal definition).
2. Update means to reflect points assigned to the cluster (see Step 3.2, below, for formal definition).

Step 3.1: Assign each point to the closest mean

\[ S_i^{(t)} = \{ x_p : \vert\vert x_p - m_i^{(t)} \vert\vert^2 \leq \vert\vert x_p - m_j^{(t)} \vert\vert^2 \,\forall\, j, 1 \lt j \lt k \}\]

At time \(t\), each set, \(S_i\), contains all the points, \(x_p\) for which its mean, \(m_i^{(t)}\), is the nearest of possible cluster means.

Step 3.2: Update means to reflect points in the cluster

\[ m_i^{(t+1)} = \frac{1}{\vert S_i^{(t)} \vert} \sum_{x_j\in S_i^{(t)}} x_j \]

At time \(t+1\), each cluster mean \(m_i^{(t+1)}\) is the centroid of the points, \(x_j\) assigned to the cluster at time \(t\).

Let’s just get it to run!

For our first step, let’s see if we can “just get the job done.” With that in mind, we’ll limit the number of features to two, x and y.

## convert data to matrix to make our lives easier (x and y, only, for now)
dat <- df %>% select(x, y) %>% as.matrix()

As the first step, we need to pick some means. We’ll do this by sampling 3 numbers between 1 and the number of rows in the data frame (1,500). Next we’ll use these to pull out three rows that will be our starting means.

## get initial means to start
index <- sample(1:nrow(dat), 3)           # give k random indexes
means <- dat[index,]

## show
means

##             x         y
## [1,] 34.14530  46.55099
## [2,] 54.79329  62.33907
## [3,] 10.76755 -17.75347

Next, we need to keep track of how we assign each point. To that end, we will first initialize an empty numeric vector with a spot for each point, assign_vec. After that, we’ll loop through each point, compute the distance between that point and each mean, and put the index of the closest mean (effectively the label) in the point’s spot in assign_vec. For example, if the first point is closest to the first mean, assign_vec[1] == 1; if the 10th point is closest to the third mean, assign_vec[10] == 3, and so on.

## init assignment vector
assign_vec <- numeric(nrow(dat))

## assign each point to one of the clusters
for (i in 1:nrow(dat)) {
  ## init a temporary distance object to hold k distance values
  distance <- numeric(3)
  ## compare to each mean
  for (j in 1:3) {
    distance[j] <- sum((dat[i,] - means[j,])^2)
  }
  ## assign the index of smallest value,
  ## which is effectively cluster ID
  assign_vec[i] <- which.min(distance)
}

## show first few
assign_vec[1:20]

##  [1] 1 3 2 1 3 3 1 1 3 3 1 2 1 2 1 1 1 3 3 1

Quick exercise

Merge the assignments back to the data (everything should be in order for a quick cbind() or bind_cols()) and then plot, assigning a unique color to each group. How did we do the first iteration?

Okay, we’ve started, but our means were arbitrary and probably weren’t the best. Now we need to pick new means and repeat the code above. We need to keep doing this until the assignments don’t change.

A while() loop is perfect for this task. We’ll create a variable called identical, which will take the Boolean FALSE. While identical is not FALSE (i.e., TRUE), the loop will continue.

Inside, we’ll compute new means, store the assignments in another object so that we can compare later, run the same code as above again, then compare the old and the new. If the old and new assignments are different, then identical remains FALSE and the loop runs again. If the old and new assignments are the same, however, identical becomes TRUE and the loop stops because !TRUE == FALSE.

## repeat above in loop until assignments don't change
identical <- FALSE
while (!identical) {
  ## update means by subsetting each column
  ## by assignment group, taking mean
  for (i in 1:3) {
    means[i,] <- colMeans(dat[assign_vec == i,])
  }
  ## store old assignments, b/c we need to compare
  old_assign_vec <- assign_vec
  ## assign each point to one of the clusters
  for (i in 1:nrow(dat)) {
    ## init a temporary distance object
    ## to hold k distance values
    distance <- numeric(3)
    ## compare to each mean
    for (j in 1:3) {
      distance[j] <- sum((dat[i,] - means[j,])^2)
    }
    ## assign the index of smallest value,
    ## which is effectively cluster ID
    assign_vec[i] <- which.min(distance)
  }
  ## check if assignments change
  identical <- identical(old_assign_vec, assign_vec)
}

Let’s check to see how we did.

## check assignment with scatter plot
plot_df <- bind_cols(df, as.data.frame(assign_vec))
g <- ggplot(plot_df, mapping = aes(x = x, y = y,
                                   color = factor(assign_vec))) +
  geom_point()

## show
g

plot of chunk programming_two_spaghetti

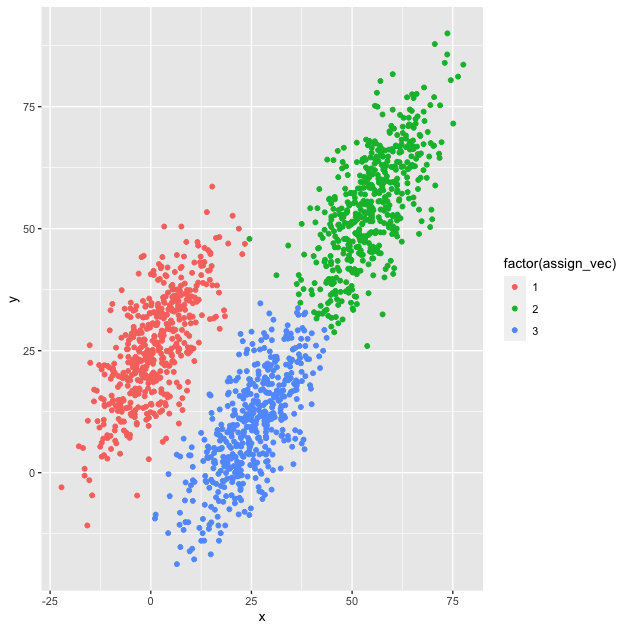
Looks like we did it! The clusters are, well, clustered and the points, for the most part, seem to be labeled correctly.

Quick exercise

The k-means algorithm can be sensitive to the starting points since it finds locally optimal solutions (no guarantee that the solution is the best of all possible solutions). Run the code again a couple of times and see how your fit changes. Do some points move between groups?

Problems

Our success not withstanding, we have a number of problems:

We have exactly repeated code
Magic numbers in the code (3)
Variable names that depend on working environment
Primary purpose of code is obfuscated

Problems 1-3 make it difficult to change things in the code. We have to remember and find each repeated instance that we want to change. Problem 3 makes it difficult to re-use the code in another script (who knows what global variables are currently lurking and, once gone, will mess up our program?).

Problem 4 means that it will be difficult to see what we did when coming back to the code in the future. With the repeated steps and the loop, it will be easy to lose the forest for the trees. What’s the point of this section of code again? After reading through multiple lines, we’ll see, if we’re lucky, that we were running a k-means clustering algorithm. That’s wasted time.

Convert to functions

What we need is to convert our spaghetti code to DRY (don’t repeat yourself) code. Each unique bit of code should be wrapped in function that does one thing and does it well. Since functions can use other functions, we can start at the smallest part and build up to something more complex.

What do we need? Looking at the code above, it looks like we would benefit from having unique functions to:

compute squared Euclidean distance
compute new means based on assignment labels
make new cluster assignments for each point

Euclidean distance function

## Euclidean distance^2
euclid_dist_sq <- function(x,y) return(sum((x - y)^2))

Compute means

## compute new means for points in cluster
compute_mean <- function(data, k, assign_vec) {
  ## init means matrix: # means X # features (data columns)
  means <- matrix(NA, k, ncol(data))
  ## for each mean, k...
  for (i in 1:k) {
    ## ...get column means, restricting to cluster assigned points
    means[i,] <- colMeans(data[assign_vec == i,])
  }
  return(means)
}

Make new assignments

Notice that we’ve added a bit to our code above. We might find it useful to compute the within-cluster sum of squares (WCSS), so we’ve added and object, wcss, that has one spot for each cluster and holds a running total of the sum of squares within each cluster.

To return multiple objects from a function, R requires that they be stored in a list. This function will return both the assignments for each point, like before, as well as the WCSS.

## find nearest mean to each point and assign to cluster
assign_to_cluster <- function(data, k, means, assign_vec) {
  ## init within-cluster sum of squares for each cluster
  wcss <- numeric(k)
  ## for each data point (slow!)...
  for (i in 1:nrow(data)) {
    ## ...init distance vector, one for each cluster mean
    distance <- numeric(k)
    ## ...for each mean...
    for (j in 1:k) {
      ## ...compute distance to point
      distance[j] <- euclid_dist_sq(data[i,], means[j,])
    }
    ## ...assign to cluster with nearest mean
    assign_vec[i] <- which.min(distance)
    ## ...add distance to running sum of squares
    ## for assigned cluster
    wcss[assign_vec[i]] <- wcss[assign_vec[i]] + distance[assign_vec[i]]
  }
  return(list("assign_vec" = assign_vec, "wcss" = wcss))
}

BONUS: standardize data

Many machine learning algorithms perform better if the covariates are on the same scale. We’ve not really had to worry about this so far since our data are scaled roughly the same. That said, we may want to use this algorithm in the future with data that aren’t similarly scaled (say, on data with age in years and family income in dollars).

This function simply standardizes a matrix of data and returns the scaled data along with the mean and standard deviations of each column (feature), which are useful for rescaling the data later.

## standardize function that also returns mu and sd
standardize_dat <- function(data) {
  ## column means
  mu <- colMeans(data)
  ## column standard deviations
  sd <- sqrt(diag(var(data)))
  ## scale data (z-score); faster to use pre-computed mu/sd
  sdata <- scale(data, center = mu, scale = sd)
  return(list("mu" = mu, "sd" = sd, "scaled_data" = sdata))
}

K-means function

Now that we have the pieces, we can put the pieces together in single function. Our function takes the following arguments:

data: a data frame (converted to matrix inside the function)
k: number of clusters we want
iterations: a stop valve in case our algorithm doesn’t want to converge
nstarts: a new feature that says how many times to start the algorithm; while not perfect it may help prevent some sub-optimal local solutions
standardize: an option to standardize the data

Note that only data and k have to be supplied by the user. The other arguments have default values. If we leave them out of the function call, the defaults will be used.

## k-means function
my_kmeans <- function(data,                  # data frame
                      k,                     # number of clusters
                      iterations = 100,      # max iterations
                      nstarts = 1,           # how many times to run
                      standardize = FALSE) { # standardize data?
  ## convert to matrix
  x <- as.matrix(data)
  ## standardize if TRUE
  if (standardize) {
    sdata <- standardize_dat(data)
    x <- sdata[["scaled_data"]]
  }
  ## for number of starts
  for (s in 1:nstarts) {
    ## init identical
    identical <- FALSE
    ## select k random points as starting means
    means <- x[sample(1:nrow(x),k),]
    ## init assignment vector
    init_assign_vec <- rep(NA, nrow(x))
    ## first assignment
    assign_wcss <- assign_to_cluster(x, k, means, init_assign_vec)
    ## iterate until iterations run out
    ## or no change in assignment
    while (iterations > 0 && !identical) {
      ## store old assignment / wcss object
      old_assign_wcss <- assign_wcss
      ## get new means
      means <- compute_mean(x, k, assign_wcss[["assign_vec"]])
      ## new assignments
      assign_wcss <- assign_to_cluster(x, k, means, assign_wcss[["assign_vec"]])
      ## check if identical (no change in assignment)
      identical <- identical(old_assign_wcss[["assign_vec"]],
                             assign_wcss[["assign_vec"]])
      ## reduce iteration counter
      iterations <- iterations - 1
    }
    ## store best values...
    if (s == 1) {
      best_wcss <- assign_wcss[["wcss"]]
      best_centers <- means
      best_assignvec <- assign_wcss[["assign_vec"]]
    } else {
      ## ...update accordingly if number of starts is > 1
      ## & wcss is lower
      if (sum(assign_wcss[["wcss"]]) < sum(best_wcss)) {
        best_wcss <- assign_wcss[["wcss"]]
        best_centers <- means
        best_assignvec <- assign_wcss[["assign_vec"]]
      }
    }
  }
  ## convert back to non-standard centers if necessary
  if (standardize) {
    sd <- sdata[["sd"]]
    mu <- sdata[["mu"]]
    for (j in 1:ncol(x)) {
      best_centers[,j] <- best_centers[,j] * sd[j] + mu[j]
    }
  }
  ## return assignment vector, cluster centers, & wcss
  return(list("assignments" = best_assignvec,
              "centers" = best_centers,
              "wcss" = best_wcss))
}

Quick exercise

Look through the function and talk through how the function will run with the following arguments:

my_kmeans(data, 3)

my_kmeans(data, 3, standardize = TRUE)

my_kmeans(data, 3, nstarts = 10)

2 dimensions

Now that we have our proper function, let’s run it! Let’s go back to where we started, with two dimensions.

## 2 dimensions
km_2d <- my_kmeans(data = df[,c("x","y")], k = 3, nstarts = 20)

## check assignments, centers, and wcss
km_2d$assignments[1:20]

##  [1] 1 2 3 2 2 2 1 2 2 2 2 3 3 3 2 1 2 1 1 3

km_2d$centers

##            [,1]      [,2]
## [1,] 25.0407539  9.780767
## [2,]  0.7741392 25.471911
## [3,] 54.6683528 54.725368

km_2d$wcss

## [1] 88179.39 89184.79 99748.81

Notice how clear and unambiguous our code is now. We are running a k-means clustering algorithm with three clusters. We get results that tell us the assignments for each point, the centers of the clusters, and the WCSS.

3 dimensions

The nice thing about our function is that it easily scales to more than two dimensions. Instead of subsetting the data, we’ll just include it all for 3 dimensions this time.

## 3 dimensions
km_3d <- my_kmeans(data = df, k = 3, nstarts = 20)

## check centers and wcss
km_3d$assignments[1:20]

##  [1] 1 3 2 3 3 3 1 3 3 3 3 2 2 2 3 1 3 1 1 2

km_3d$centers

##            [,1]     [,2]      [,3]
## [1,] 25.2858908 10.26503 -24.21246
## [2,] 54.8865406 54.97876 105.13575
## [3,]  0.8928973 25.51276  25.58783

km_3d$wcss

## [1] 167007.1 159247.5 153343.3

Check out plots

Let’s plot our assignments. First, let’s plot the two dimensional assignments. We’ll use plotly this time so that it’s easier to zoom in on individual points.

## using 2D: looks good 2D...
p <- plot_ly(df, x = ~x, y = ~y, color = factor(km_2d$assignments)) %>%
  add_markers()

## show
p

Looks pretty much like our first plot above. But what happens if we include the third feature, z, that we ignored?

## ...but off in 3D
p <- plot_ly(df, x = ~x, y = ~y, z = ~z, color = factor(km_2d$assignments),
             marker = list(size = 3)) %>%
  add_markers()

## show
p

Ah! Not so good! Clearly, some of the points appear to fit in one cluster if only x and y are considered, but no longer do when the third dimension is included.

Quick exercise

Manipulate the 3D plotly figure to see if you can recreate the 2D plot, that is adjust the viewing angle. Then move it around to see how that flattened view was deceptive.

Let’s move to our results that used all three features. Again, we’ll first look in just two dimensions.

## using 3D: looks off in 2D...
p <- plot_ly(df, x = ~x, y = ~y, color = factor(km_3d$assignments)) %>%
  add_markers()

## show
p

In two dimensions, our clusters look a bit messy since they overlap on the edges. But looking in three dimensions…

## ...but clearly better fit in 3D
p <- plot_ly(df, x = ~x, y = ~y, z = ~z, color = factor(km_3d$assignments),
             marker = list(size = 3)) %>%
    add_markers()

## show
p

Much better! Not perfect, but better.

Quick exercise

What happens if you assume 4 or 5 groups? Run the my_kmeans() function with those options and make a plotly plot. How does it look — better fit? worse fit?

EDH 7916: Contemporary Research in Higher Education

Spring 2023

Overview
Course information
Meeting location
Software
Schedule
Lessons
Assignments
Questions
Past courses
About

Functional programming II

Load libraries and set paths

Read in and inspect data

K-means clustering

Algorithm

Step 3.1: Assign each point to the closest mean

Step 3.2: Update means to reflect points in the cluster

Let’s just get it to run!

Quick exercise

Quick exercise

Problems

Convert to functions

Euclidean distance function

Compute means

Make new assignments

BONUS: standardize data

K-means function

Quick exercise

2 dimensions

3 dimensions

Check out plots

Quick exercise

Quick exercise